0. Presentation of the Course

Exams

100%, can use any notes including internet Take hop exam

Types of Questions

• Numerical Questions
• Theoretical questions

Difficulty Levels

• 60-80 marks: questions of the same type of those solved during the lectures
• 20-40 marks: questions that require some creativity and reasoning

Topics

Mainly about algebra and calculus

• Matrices
• Systems of Linear Equations
• Vector Spaces
• Linear Mappings

1. The Basics

Basic Definitions and notation

Set is a collection of items, name elements, characterised by a certain property $A = \{ 2,4,7,D,24\}$ Element $x$ belgons to $A$ indicated as $x \in A$ Several elements of $A$ compose a subset $S:S\subset A$

Want to inidcate all the elements of the set: $\forall x \in A:$ Want to say there exists(at least) one element of $A$ which has a certain property (such that): $\exists x \in A \ni '$
Want to say there exists only/exactly one element of $A$ which has certain property $\exists! x \in A \ni '$ if statement 1 THEN statement 2 $\rightarrow$ statement 1 IF AND ONLY IF statement 2 $\iff$

Cardinality of a set

coincident - every element of $A$ is also an element of $B$ and every element of $B$ is also an element of $A$ cardinality of a set is number of elements contained in $A$ empty - indicated with $\emptyset$

Intersection and Union

intersection - $C = A \cap B$ - set containing all the elements that are both in the sets $A$ and $B$ union - $C = A \cup B$ - set containing all the elements that are either or both the sets $A$ and $B$ difference - $C = A \setminus B$ - set containing all the elements that are in $A$ but not $B$

Associativity of the Intersection

$(A\cap B) \cap C = A\cap (B\cap C)$

Numbers and Number sets

Set is finite if its cardinality is a finite number. Set is infinite if its cardinality is $\infty$ continuous if $\forall x_0 \in A:\exists x \ni ' |x-x_0|$

Types of Number Sets

Continue from last semester ℂ - Set of number than can be expressed as $a+jb$ where $a,b\in \R$ and the imaginary uni $j=\sqrt {-1}$

Cartesian Product

New set generated by all the possible pairs $C=A\times B$ $A=\{ 1,5,7\}$ $B=\{ 2,3\}$ $C=A\times B = \{ (1,2),(1,3),(5,2),(5,3),(7,2),(7,3)\}$

Relations

Order Relation

Indicated with $\preceq$ if following properties are verified:

• reflexivity
• transitivity
• antisymmetry

Example

Let $x,y \in \N$ and let consider $(x,y) \in \mathscr{R}$ if and only if $x$ is a multiple of $y$. More formally $(x,y)\in \mathscr{R}\iff \frac{x}{y} = k$ with $k\in \N$

Equivalence

Indicated with $\equiv$ if following properties are verified:

• Reflexivity - $x \equiv x$
• symmetry - $x\equiv y$ then $y\equiv x$
• transitivity - $x\equiv y$ and $y\equiv x$ then $x \equiv z$

Equivalence Classes

Let $\mathscr{R}$ be an equivalence relation defined on $A$. The equivalence class of an element $a$ is a set defined as $[a]=\{ x \in A|x \equiv a \}$

Partition

Set of all the elements equivalent to $a \in A$ is called equivalence class and is indicated with $[a]$

Functions/Mapping

Relation is to be a mapping or function when it relates to any element of a set unique element of another. Let $A$ and $B$ be two sets, a mapping $f:A \to B$ is a relation $\mathscr{R} \subseteq A\times B$ such that: $\forall x \in A\exists! y \in B\ni '(x,y) \in \mathscr{R}$ (Every element, find only 1 element in other set such that y is = x)

The statement $(x,y) \in \mathscr{R}$ can be expressed also as $y=f(x)$ Unary operator - $f:A \to B$ Binary operator - $f:A \times A \to B$ or $f:A\times C\to B$ Internal composition law - $f:A\times A\to A$

algebraic structure - set endowed with 1+ internal composition laws $(A,+,.)$

Injective Functions

$f A \to B$ is injection if the function values of two different elements is always different: $\forall x_1$ and $\forall x_2$ if $x_1 \ne x_2$ then $f(x_1) \ne f(x_2)$ Never crosses horizontal line twice. Doesnt cross it twice

Surjective Functions

$f A \to B$ is surjective if all elements of $B$ are mapped by an element of $A: \forall y\in B$ it follows that $\exists x \in A$ such that $y=f(x)$ Graph has no holes. Y axis as got a function, eg crosses graph

Bijective Functions

$f A \to B$ is bijective when both injection and surjection are verified

Numeric Vector

Numeric Vector

• Let $n\in \N$ and $n>0$
• Indicated with $\R^n$, set of ordered n-tuples of real numbers
• Generic element a = ($a_1,a_2,...,a_n$) is named numeric vector or simply vector of order n

Sum of Vectors

• Sum of vectors: $c = (a_1 + b_1 , a_2 + b_2 , . . . , a_n + b_n )$
• Can also do the same for $a-b$

Scalars

Numeric value $\lambda \in \R^1$ is a scalar The product of a vector by a scalar is the vector $c=(\lambda a_1,\lambda a_2,...,\lambda a_n)$ Very similar to $\times$

Scalar Product

Generated by the sum of the products of each pair of corresponding components $ab = c = a_1b_1 + a_2b_2,...,a_nb_n$ Example:

• $a = (1, 0, 3)$
• $b = (2, 1, −2)$
• $ab = (1 · 2) + (0 · 1) + (3 · (−2)) = 2 + 0 − 6 = −4$

Properties

• Symmetry: $ab=ba$
• Associativity: $\lambda (ba) = (\lambda a)b = a(\lambda b)$
• Distributivity: $a(b+c)=ab+ac$

Matrices

Matrix

2 natural numbers > 0. A matrix ($m\times n$) is a generic table of the kind

$A=\begin{pmatrix} a_1,_1&a_1,_2&...&a_1,_n \\ a_2,_1&a_2,_2&...&a_2,_n \\ ...&...&...&...\\ a_m,_1&a_m,_2&...&a_m,_n \\ \end{pmatrix}$ where each matrix element $a_i,_j\in \R$

• m=rows, n=columns
• n order square matrix - $A \in \R_n,_n$
• rectangular - $m \ne n$

Matrix Transpose

• Transpose matrix is $A^T$ whose elements are the same of A but $\forall i,j : a_j,_i = a^T_i,_j$
• Change index of row with index of columns (rotate it)

Symmetry

• Only on square matrix
• When $\forall _i,_j : a_i,_j = a_j,_i$

Diagonal and Trace

• Diagonal of a matrix is the ordered n-tuple that displays the same index twice. From 1 to $n a_i,_j$
• Trace is the sum of the diagonal elements tr($A$)

Null Matrices

• Is said null $O$ if all elements are zeros

Identity Matrices

• Square matrix whose diagonal elements are all ones while all the other extra-diagonal elements are zero

Matrix Operations: Sum and Product

Matrix Sum

$\forall i,j:c_i,_j = a_i,_j + b_i,_j$ Both matrices must be the same size! Can be subtracted from one another

Properties of the matrix sum

• commutativity: $A + B = B + A$
• associativity: $(A + B) + C = A + (B + C)$
• neutral element: $A + O = A$
• opposite element: $∀A ∈ Rm,n : ∃!B ∈ R m,n \ni ‘ A + B = O$

Product of a scalar and a matrix

Matrix $C$ defined as: $\forall i,j:c_i,_j = \lambda a_i,_j$ Similar to $\times$ by the scalar

Properties of multiplying by a scalar

• associativity: $\forall A \in \R_m,_n$ and $\forall \lambda , \mu \in \R$:
  • $(\lambda \mu )A = (A\mu ) \lambda = (A \lambda) \mu$

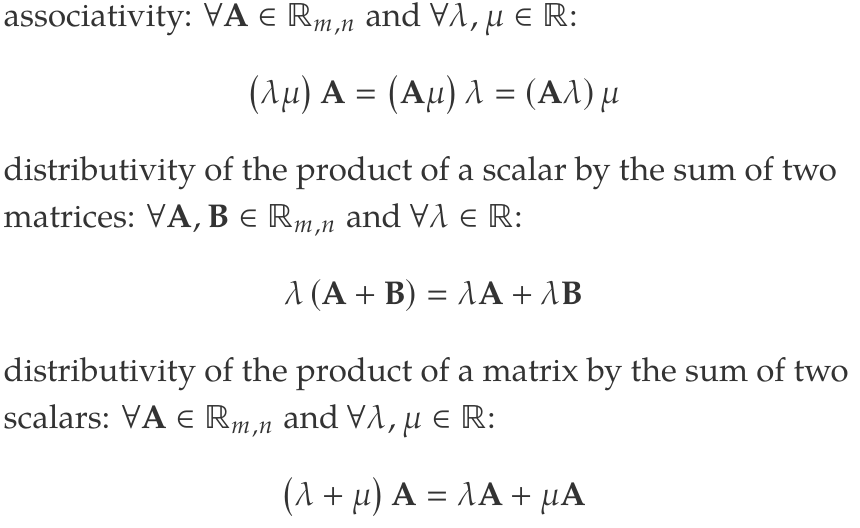
Matrix product

Product of matrices $A$ and $B$ is a matrix $C = AB$

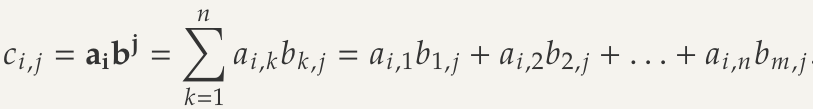
• Just the scalar product of row vectors of $A$ with column vectors of $B$
• Number of columns in the first matrix must be the same as the number of rows in the second

$c_2,_1 = a_2b^1$

• left distributivity: $A (B + C) = AB + AC$
• right distributivity: $(B + C) A = BA + CA$
• associativity: $A (BC) = (AB) C$
• transpose of the product: $(AB)^T = B^T A^T$
• neutral element: $\forall A : AI = A$
• absorbing element: $\forall A : AO = O$

Commutable - $AB=BA$, one with respect to the other Every matrix $A$ is commutable with $O$ (and the result is always $O$) and with $I$ (and the result is always $A$)

Determinant of a Matrix

(takes decades to understand)

• Most important concepts of maths

• Permutation: Different ways of grouping items, can be checked with factorials
• Fundamental Permutation - Reference a sequence
• Inversion - Every time two objects in a permutation follow each other in a reverse order with respect to the fundamental
• Even class permutation - Permutation undergone to an even number of inversions
  • Also have Odd class permutation

Associated Product

Never in the same column/row. Product of this is referred to as associated product and is indicated with the symbol $\epsilon$(c). Wont be the same number either. Order the factors according to the row index:

Coefficient of nk

Consider 1-2-...-n as fundamental permutation, the scalar nk is defined as:

Determinant of a Matrix

indicated as det $A$ is the function det: $\R_n,_n \to \R$ defined as the sum of n! associated products: $\sum ^{n!} _{k=1} ....$ Do it as left to right diagonal +, then right to left diagonal as -

Linear Dependence/Independence

Linear Combination

If row can be represented by other rows with weighted sum by means of the same scalars

Linear dependence

If null vector can be expressed as the linear combination of the $m$ rows ($n$ columns) by means of nun-null scalars Rows are linearly dependent if

$\exists \lambda_1,\lambda_2,...,\lambda_m\ne0,0,...,0$ such that

Linear Independence

If only way to express a row of all zeros as the linear combination of the m rows(n columns) is by means of null scalars

Fundamental property of Linear Dependence

r rows are linearly dependent if and only if at least one row can be expressed as the linear combination of the others

Properties of determinants

Determinant of a matrix $A$ is equal to the determinant of its transpose matrix

• Transpose Matrix: $detA = det A^T$
• Triangular Matrix: Equal to the product of the diagonal elements
• Row(Column) swap: If two rows (columns) are swapped the determinant of the matrix $A_s$ is $-detA$
• Null determinant: if two rows(columns) are identical(sum) then $detA=0$
  • If and only if the rows(columns) are linearly dependent
  • if and only if at least one row(column) is a linear combination of the other rows(columns)
  • if a row(column) is proportional to another row(column)
• Invariant Determinant: Row(column) the elements of another row(column) all multiplied by the same scalar are added, the determinant remains the same
• Row(column) multiplied by a scalar: Row(column) is multiplied by $\lambda$ then $\lambda detA$
• Matrix multiplied by a scalar: If $\lambda$ is scalar, $det(\lambda A) = \lambda ^n detA$
• Determinant of the product: Product between two matrices is equal to the products of the determinants. $det(AB) = det(A)det(B) = det(B)det(A) = det(BA)$

Adjugate Matrices

Submatrix

Obtained from $A$ by cancelling $m-r$ rows and $n-s$ columns. Where r,s 2 positive integers such that $1\le r \le m$ and $1\le s\le n$

• Rows dont have to be continuous
• $A=\begin{pmatrix} 3&3&1&0\\ 2&4&1&2\\ 5&1&1&1\\ \end{pmatrix}$
• Can be obtained by cancelling the second row, second and fourth column
• $\begin{pmatrix} 3&1\\ 5&1 \\ \end{pmatrix}$

---

• Minor: Determinant of submatrix
• Major: If submatrix is the largest square
• Complement submatrices: Obtained by cancelling on the $i^{th}$ row and the $j^{th}$ column from $A$ to the element $a_{i,j}$
• Complement Minor: Determinant, indicated $M_{i,j}$
• Cofactors: $A_{i,j} = (-1)^{i+j}M_{i,j}$

Adjugate Matrix

$A=\begin{pmatrix} a_{1,1}&a_1,_2&...&a_1,_n \\ a_2,_1&a_2,_2&...&a_2,_n \\ ...&...&...&...\\ a_n,_1&a_n,_2&...&a_n,_n \\ \end{pmatrix}$

Let $A_{i,j}$ be the cofactor for $a_{i,j}$. The adjugate matrix (adjunct or adjoin) $A$ is: $adj(A)=\begin{pmatrix} A_1,_1&A_2,_1&...&A_n,_1 \\ A_1,_2&a_2,_2&...&A_n,_2 \\ ...&...&...&...\\ A_{1,n}&A_{2,n}&...&A_{n,n}\\ \end{pmatrix}$

Dan Terms: Transpose it (Flip i,j around), then calculate the determinate of the remaining rows once removed it(the sub matrix, as would do normally). Then alternate between 1 and -1.(Use cofactors formula!. $(-1)^{i+j}$)

Tutorial Def:

1. $A$
2. $A^T$
3. All Compliment miners
4. Multiple by coefficent = adjudigate matrix
5. $A^{-1} = \frac{1}{detA}\times adj(A)$

Laplace Theorems

Theorem 1

Determinant of $A$ can be computed as the sum of each row(column) multiplied by the corresponding cofactor $det A = \sum ^n _{j=1} a_{i,j} A_{i,j}$ for any arbitrary $i$ $det A = \sum ^n _{i=1} a_{i,j} A_{i,j}$ for any arbitrary $j$

The determinant of a one-element matrix is just the element $(det(a = a))$, can compute the determinant of any square number

Theorem 2

Sum of the elements of a row(column) multiplied by the corresponding cofactor related to another row(column) is always zero $\sum ^n _{j=1} a_{i,j} A_{k,j}=0$ for any arbitrary $k\ne i$ $\sum ^n _{i=1} a_{i,j} A_{i,k}=0$ for any arbitrary $k\ne j$

minors are the row you remove, so you take sub matrix of the remaining part. $k$ = minor

Introduction to Matrix inversion

Inverting a matrix

For a square matrix, $A$, the inverse is $A^{-1}$ which is define as the matrix for which $AA^{-1}=I$

• Invertible Matrices: $\exists$ a matrix $B \in \R _{n,n} | AB=I=BA$
• Unique Inverse $\exists!$ a matrix $B \in \R _{n,n} | AB=I=BA$
• Inverse matrix $A^{-1}$: $A^{-1} = \frac{1}{detA} adj(A)$
• Singular/Non Invertable/ Linear Dependent: $det(A) =0$
• Non-singular: $det(A)\ne 0$
• Inverse of a matrix product: $(AB)^{-1}=B^{-1}A^{-1}$

Orthogonal Matrices

$A\in \R_{n,n}$ is said orthogonal if the product between it and its transpose is the identity matrix:

$AA^T = I = A^TA$

An orthogonal matrix is always non-singular and its determinant is either 1 or -1

A matrix is orthogonal if and only if the ssum of the squares of the element of a row(column) is equal to 1 and the scalar product of any two arbitary rows(columns) is equal to 0: $\sum^n_{j=1}a^2_{i,j} =1$ $\forall i,j a_ia_j=0$

Rank of a Matrix

Rank - $A\in \R_{m,n}$ of matrix $A$, indicated as $\rho_A$ is the highest order of the non-singular submatrix $A_ρ \subset A$. So max value of rank in 3x3 matrices would be 3. If there is linear independence, then go to 2x2 and so forth. If $A$ is the null matrix then its rank is taken equal to 0

$A\in \R_{n,n}$ Matrix $A$ has ρ linearly independent rows(columns).

Rank is c

Sylvester's Lemma

$A\in \R_{n,n}$ and $B\in \R_{n,q}$. Let $A$ be non-singular and $ρ_B$ be the rank of the matrix $B$. Follows that the rank of the product matrix $AB$ is $ρ_B$

Law of Nullity

follows from the previous lemma $ρ_A$ and $ρ_B$ be the ranks and $ρ_{AB}$ be rank of the product AB. FOllows that: $ρ_{AB}\ge ρ_A+ρ_B-n$

Systems of Linear Equations

Basically simultaneous equations. Can be written as $Ax=b$

The coefficient matrix $A$ is said incomplete matrix. The matrix $A^c\in \R_{m,n+1}$ whose first $n$ columns are those of the matrix $A$ and the $(n+1^{th})$ column is the vector $b$ is said complete matrix

$A^c=(A|b)=$

Cramer's Theorem

If $A$ is non-singular , the is only one solution simultaneously satisfying all the equations: if $detA\ne 0$ then $\exist!x$ such that $Ax=b$

Hybrid Matrix

Hybrid matrix with respect to the $i^{th}$ column is the matrix $A_i$ obtained from $A$ by substituting the $i^{th}$ column with $b$ (Switch $a^i$ with $b$)

Cramer's Method

For a given system of linear equations $Ax=b$ with $A$ non-singular, a generic solution $x_i$ element of $x$ can be computed as $x_i=\frac{detA_i}{detA}$

For a square matrices would repeat 3 times, change column 3 times with $b$

Rouchè-Capelli Theorem

Solutions for systems of linear equations

• compatible if it has at least one solution
• determined if it has only one solution
• undetermined if it has infinite solutions
• incompatible if it has no solutions. Has a split $A^c=A|b$

Theorem

$Ax=b$ is compatible if and only if both the complete and incomplete matrices ($A|A^c$) are characterised by the same rank $\rho_A = \rho_{A^c}=\rho$ named rank of the system

Cases

$\rho_a<\rho_{a^c}$ - Incompatible, no solutions $\rho_a=\rho_{a^c}$ - system is compatible. Under these conditions, three cases can be identified:

1. $\rho_a=\rho_{a^c}=\rho=n=m$ - System is a Cramers system and can be solved Cramers method
2. $\rho_a=\rho_{a^c}=\rho=n<m, \rho$ equations of the system compose a Cramers system. The remaining $m-\rho$ are linear combination of the other, these equations are redundant and only 1 solution
3. $\rho_a=\rho_{a^c}=\rho\begin{cases}< n\\\le m\end{cases}$ is undetermined and has $\infty^{n-\rho}$

How to choose the equations to cancel?

• Cannot cancel any equations
• Need to ensure that the cancellation of an equation does not change the rank of the incomplete matrix $A$
• Have to cancel only linearly dependent equations, that is rows of the matrix $A^c$

General Solutions of Undetermined Systems

• Select the $\rho$ rows linearly independent rows of the complete matrix $A^c$
• Choose (arbitrarily) $n-\rho$ variables and replace them with parameters
• Solve the system of linear equations with respect to the remaining variables
• Express the parametric vector as a sum of vectors, where each parameter appears in only one vector

Homogeneous Systems of Linear Equations

Homogeneous if the vector of known terms $b$ is composed for only zeros and is indicated with O. Solution of at least null vector

General solution of a system

If a solution of the homogeneous system then $\lambda$ is also a solution to the system

Combination of solutions

If $\alpha$ and $\beta$ are both solutions then every linear combination of these two n-tuple is solution of the system. $\forall\lambda,\mu\in\R.(\lambda\alpha_1+\mu\beta_1,\lambda\alpha_2+\mu\beta_2,...,\lambda\alpha_n+\mu\beta_n)$

Special Property

Homogeneous system of $n$ equations in $n+1$ variables. System has $\infty^1$ solutions proportionate to the n-tuple

• Cramers Method requires the calculation of 1 determinant of a $n$ order matrix and $n$ determinate of $n$ order matrices
• Means $n!+n(n!)$ elementary operations
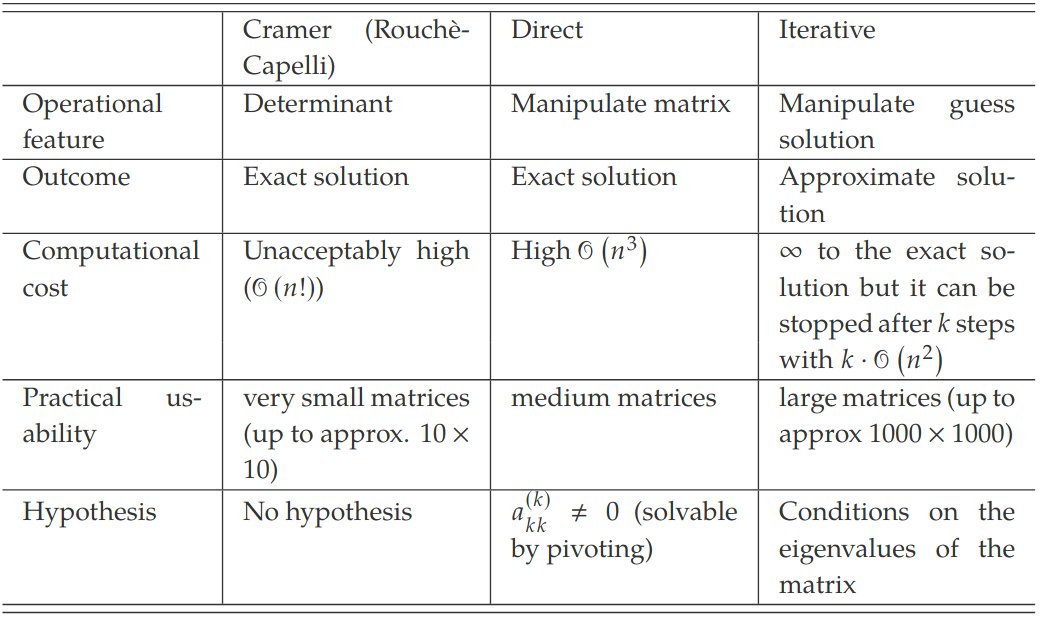
• Need to find alternative methods as takes too long

Theoretical Foundations of Direct Methods

Elementary Row Operations

• $E_1$: Swap of two rows $a_i$ and $a_j$$a_i \leftarrow a_j$$a_j \leftarrow a_i$
• $E_2$: Multiplication of a row $a_i$ by a scalar $\lambda\in\R$$a_i\leftarrow\lambda a_i$
• $E_3$: Substitution of a row $a_i$ by the sum of the row $a_i$ to another row $a_j$: $a_i\leftarrow a_i+a_j$

Equivalent Matrices and Equivalent Systems

Equivalent Matrices: Apply the elementary row operations on $A$, obtain new matrix $C\in\R_{m,n}$.

Equivalent Systems: 2 systems of linear equations in the same variables: $Ax=b$ and $Cx=d$. These two systems are equivalent if they have the same solutions

Consider a system of $m$ linear equations in $n$ variables $Ax=b$. Let $A^c\in\R_{m,n+1}$ be the complete matrix associated with this system. If another system of linear equations is associated with a complete matrix $A^{'c}\in\R_{m,n+1}$ equivalent to $A^c$, then the two systems are equivalent

• $E_1$: The swap of two rows, the equations of the system are swapped, no effect on the solution of the system
• $E_2$: Same solutions, modified systems is equivalent to the original one
• $E_3$: After operation, the modified system is equivalent in solutions to the original one

Direct Methods

Direct methods are methods for solving systems of linear equations by manipulating the original matrix to produce an equivalent system that can be easily solved. A typical manipulation is the transformation of a system of linear equation into triangular system

Gaussian Elimination

$Ax=b$

1. Construct the complete matrix $A^c$
2. Apply the elementary row operations to obtain a staircase complete matrix and triangular incomplete matrix, that is we add rows to obtain a null element in the desired position
3. Write down the new system of linear equations
4. Solve the $n^{th}$ equations of the system and use the result to solve the $(n-1)^{th}$
5. Continue recursively until the first equation

To obtain the matrix would do: $r^{(2)}_2=r^{(1)}_2+(\frac{-a^{(1)}_{2,1}}{a^{(1)}_{1,1}})\times r^{(1)}_1$ As it keeps going on, it gets longer and longer, to create a matrices with leading zeros

Dan Method: $a_{n,m}-(a_{n,1}\times a_{n-1,m})$ This completes the first 2 rows and first column. Then have to increase m, to do second column

LU factorisation

Direct method that transforms a Matrix into a matrix product $LU$ where $L$ is a lower triangular matrix having the diagonal elements all equal to 1 and $U$ is an upper triangular matrix $Ax=b\Rightarrow LUx=b$ Pose $Ux=y$ solve at first the triangular system $Ly=b$ and then extract $x$ from the triangular system $Ux=y$ Does not alter the vector of known terms $b$.

If working with non singular matrix, then split any matrix into a product such that $A=LU$. If non-singular matrix and is square, and has det of 0, then $\exists!$ lower traingular matrix $L$ having all the diagonal elements equal to 1 and $\exists!$ upper triangular matrix $U$ such that $A=LU$

Equivalence of Gaussian elimination and LU factorisation

• Gaussian elimination and LU factorisation are both direct methods
• They are not identical but they are equivalent
• Whilst performing the algorithm the LU factorisation is implicitly performed
• Both Gaussian elimination and LU factorisation have a lower complexity than theoretical methods
• The complexity is in the order of $n^3$ operations

Short introduction to Iterative Methods

Jacobi's Method - Starts from an initial guess $x^{(0)}$, iteratively apply some formulas to detect the solution of the system. Unlike direct methods that converge to the theoretical solution in a finite time, iterative methods are approximate since they converge, under some conditions

Definition of Vector Space

Vector Space

• $E$ to be a non-null set and $K$ to be a scalar set
• Vectors: elements of the set $E$
• $+$ - Internal composition law, $E\times E \to E$
• $.$ - External composition law, $K\times E\to E$
• ($E,+,.$) is said vector space of the vector set $E$ over the scalar field ($K,+,$) if and olf if the ten vector space axioms are verified

Axioms

• $E$ is closed with respect to the internal composition law: $∀u, v ∈ E : u + v ∈ E$
• $E$ is closed with respect to the external composition law: $∀u ∈ E and ∀λ ∈ K : λu ∈ E$
• Commutativity for the internal composition law: $∀u, v ∈ E : u + v = v + u$
• Associativity for the internal composition law: $∀u, v, w ∈ E × E : u + (v + w) = (u + v) + w$
• Neutral element for the internal composition law: $∀u ∈ E : ∃!o ∈ E|u + o = u$
• Opposite element for the internal composition law: $∀u ∈ E : ∃!−u ∈ E|u + −u = o$
• Associativity for the external composition law: $∀u ∈ E$ and $∀λ, μ ∈ K : λ(μu) = (λμ) u = λμu$
• Distributivity 1: $∀u, v ∈ E$ and $∀λ ∈ K : λ (u + v) = λu + λv$
• Distributivity 2: $∀u ∈ E and ∀λ, μ ∈ K : (λ + μ)u = λu + μu$
• Neutral elements for the external composition law: $∀u ∈ E : ∃!1 ∈ K |1u = u$

Vector Subspace

($E,+,.$) be a vector space, $U \subset E$ and $U \ne ∅$ The triple ($E,+,.$) is a vector subspace of ($E,+,.$) if ($U,+,.$) is a vector space over the same field $K$ with respect to both the composition laws

Proposition shows that we do not need to prove all 10 axioms, just need to prove closure of the two composition laws.

Null vector in Vector Spaces

($E,+,.$) be a vector space over a field $K$. Every vector subspace ($U,+,.$) of ($E,+,.$) contains the null vector. For every vector space ($E,+,.$), at least two vector subspace exist

Intersection and Sum Spaces

Intersection Spaces

If ($U,+,.$) and ($V,+,.$) are two vector subspace of ($E,+,.$), then ($U\cap V,+,.$) is a vector subspace of ($E,+,.$)

Sum Space

($U,+,.$) and ($V,+,.$) be a vector space of ($E,+,.$). Sum subset is a set $S=U+V$ defined as $S=U+V=\{ w\in E |\exists u \in U, v \in V|w=u+v \}$

Direct Sum

($U,+,.$) and ($V,+,.$) be two vector subspaces of ($E,+,.$). If $U\cap V = \{ o\}$ the subset sum $S=U+V$ is indicated as $S=U⊕V$ and named subset direct sum

Linear dependence in $n$ dimensions

Basic Definition

• Linear combination of the $n$ vectors by means of $n$ scalars is the vector $\lambda_1v_1+\lambda_2v_2+...+\lambda_nv_n$
• Said to be linear dependent if the null vector o can be expressed as linear combination by means of the scalars $\lambda_1,\lambda_2,...,\lambda_n\ne 0,0,...,0$
• Vectors are linearly independent if the null vector $o$ can be expressed as linear combination only by means of the scalars $0,0,...,0$
• Are linearly dependent if and only if at least one of them can be expressed as linear combination of the others
• Would then check them as you would do in matrices

Linear Span

Set containing the totality of all the possibly linear combinations of the vectors, by means of $n$ scalars. $L (v_1 , v_2 , . . . , v_n ) = \{ λ_1 v_1 + λ_2 v_2 + . . . + λ_n n |λ_1 , λ_2 , . . . , λ_n ∈ K \}$

Properties

1. Span $L(v_1,v_2,...,v_n)$ with the composition laws in a vector subspace of ($E,+,.$)
2. $s\in \N$ with $s<n$. If $s$ vectors are linearly independent while each of the remaing $n-s$ vectors is linear combination of the linearly independent $s$ vectors, then $L (v_1 , v_2 , . . . , v_n ) = L (v_1 , v_2 , . . . , v_s )$
3. $L (v_1 , v_2 , . . . , v_n ) = L (v_{(σ)1} , v_{(σ)2} , . . . , v_{(σ)no })$

Basis of a Vector Space

Basis

Vector space is said to be finite-dimensional if $\exists$ a finite number of vectors such that the vector space $(L,+,.)=(E,+,.)$ where the span $L$ is $L(v_1..)$.

A basis $B=\{v_1...\}$ of $(E,+,.)$ is a set of vectors $\in E$ that verify the following properties:

• They are linearly independent
• They span $E$, i.e. $E = L(v_1..)$

Null Vector and Linear Dependence

If one of the vectors is equal to the null vector, then these vectors are linear dependent

Steinitz Lemma

$(E,+,.)$ = Finite-dimensional vector space $L(v_1..)=E$ = E its span Let $w_1...$ be $s$ linearly independent vectors $\in E$ Follows that $s\le n$, the number of a set of linearly independent vectors cannot be higher than the number of vectors spanning the vector space.

Corollary of the Steinitz Lemma

^continuation $B=\{w_1...\}$ be its basis, it follows that $s\le n$. The vectors composing the basis are linearly independent. For the Steinitzs Lemma, it follows immediately that $s\le n$

Dimension of a Basis

Order of a Basis

Number of vectors composing a basis is said order of a basis All the bases of a vector spaces have the same order

Dimension of a Vector Space

The order of a basis is said dimension is indicated with dim $(E,+,.)$ or dim($E$). The dimension dim $(E,+,.)=n$ of a vector space is:

• the maximum number of linearly independent vectors of E
• the minimum number of vectors spanning E

Linear independence and dimension

The vectors span the vectors if and only if they are linearly independent

Grassmann Formula

Reduction and Extension of a basis

Basis Reduction Theorem - If some vectors are removed a basis of $(E,+,.)$ is obtained Basis Extension Theorem - Let $w_1..$ be $s$ linearly independent vectors of the vector space. If $w_1..$ are not already a basis, they can be extended to a basis (by adding other linearly independent vectors)

Unique Representation

If the $n$ vectors are linearly dependent while $n-1$ is linearly independent, there is a unique way to express one vectors as linear combination of others (How you would represent other lines with one another, identify them with lambdas)

Grassmanns Formula

Let $(U,+,.)$ and $(V,+,.)$ be vector subspace of $(E,+,.)$. Then, $dim(U+V)+dim(U\cap V) = dim(U) + dim(V)$

Basic Definitions of Mappings

Mapping and Domain

$U$ be a set such that $U\subseteq E$ The relation $f$ is said mapping when $\forall u\in U : \exists!w\in F \ni`f(u)=w$ Said domain and is indicated with $dom(f)$

A vector $w$ such that $w=f(u)$ is said to be the mapped (or transformed) of $u$ through $f$

Image

Image ($Im$) is a set of all all vectors $w$ that exist such that $f(u)=w$ $Im(f)=\{w\in F | \exist u\in E\ni`f(u)=w\}$

dom/domain = Input Image = output $\to$ also means a subset

Surjective, injective, bijective

Mapping $f$ is surjective if the image of $f$ coincides with $F:Im(f)=F$

Mapping $f$ is injective if $\forall u,v \in E$ with $f(u)=f(v)\to u=v$ (if $u$ is different from $v$, then so will $f(u)/f(v)$)

Mapping $f$ is bijective if $f$ is injective and surjective

Linear Mappings

Linear Mapping

Linear mapping if the following properties are valid:

• Additivity: $\forall u,v \exists E:f(u+v)=f(u)+f(v)$
• Homogeneity: $\forall\lambda \in K$ and $\forall v\in E :f(\lambda v)= \lambda f(v)$

(This happens very very rarely)

Affine Mapping

Said affine if $ g(v) = f(v) - f(u)$ is linear

Linear Mappings

Image of $U$ through $f$, $f(U)$ is the set $f(U)=\{w\in F | \exist u \in U \ni`f(u)=w\}$ Follows that the triple $(f(u),+,.)$ is a vectors subspace of $(F,+,.)$

Inverse Image

$E\to W\subset F$ The inverse image of $W$ through $f$, indicated with $f^{-1}(w)$ is a set defined as: $f^{-1}w=\{u\in E|f(u)\in W\}$

Matrix Representation

Linear mapping can be expressed as the product of a matrix by a vector $y=f(x)=Ax$

Image from a matrix

The mapping $y=f(x)$ is expressed as a matrix equation $y=Ax$. Follows that the image of the mapping $Im(f)$ is spanned by the column vectors of the matrix A: $Im(f)=L(a^1,a^2,...a^n)$ where $A=(a^1,a^2,...a^n)$

(Just convert matrix into (A). Columns into own (C))

Endomorphisms and Kernel

Endomorphism

$E\to F$. If $E=F$, $f:E\to E$ then linear mapping is endomorphism

Null Mapping

$O:E \to F$ is a mapping defined as $\forall v \in E: O(v) = O_F$

Identity Mapping

(Should be same dimension) $I:E\to F$ is a mapping defined as $\forall v\in E: I(v)=v$

Matrix Representation

$E\to E$ be endomorphism. Mapping of multiplication of a square matrix by a vector: $f(x):Ax$

$y=f(X)=Ax$. The inverse function $x=f^{-1}(y)=A^{-1}y$

Linear dependence

Needs to be endomorphism $v_1...$ likely dependent then so are $f(v)...$

Kernal

$E\to F$ linear mapping $ker(f)=\{v\in E| f(v) = o_F$

Kernal as Vector Space

The triple $(Ker(f),+,.)$ is a vector subspace of $(E,+,.)$

Kernal and Injection

$f:E\to F$ be a linear mapping $u,v\in E$. Follows that $f(u)=f(v)$ if and only if $u-v\in Ker(f)$

Theorem

Mapping is injective if and only if: $Ker(f)=\{o_e\}$

Linear Independence and injection

$E\to F$ $V_1.....$ be $n$ linearly independent vectors $\in E$. If $f$ is injective then $f(v_1)...$ are also linearly independent vectors of $f$ Endomorphism $f$ is invertible if and only if it is injective

Rank-Nullity Theorem

Let $f:E\to F$ be a linear mapping. The rank of $f$ is the dimension of the image, $rk(f) := dim(Im(f))$ The rank is an invariant of the map.

The dimension of the kernel, $dim(ker(f))$ is said nullity of a mapping.

Theorem

Under the hypothese: the sum of rank and nullity of a mapping is equal to the dimension of the vector space $(E,+,.)$: $dim(ker(f)) + dim(Im(f)) = dim(E)$ Usually $dim(Im(f))$ is the hardest to calculate and this theorem allows an easy way to compute it as $dim(E)-dim(ker(f))$

Proof

If $dim(ker(f))=0$ then $f$ is injective. If the basis spans the image, the vectors are linearly independent.

Corollaries of Rank-Nullity Theorem

Let $f:E\to E$ be an endomorphism where $(E,+,.)$ is a finite-dimensional vector space.

• If $f$ is injective then it is also surjective
• if $f$ is surjective then it is also injective

Corollary

Let $f:E\to F$ be a linear mapping with $(E,+,.)$ and $(F,+,.)$.

• Consider $dim(E)>dim(F)$. Follows that the mapping is not injective.
• Consider $dim(E)<dim(F)$. Follows that the mapping is not surjective

Eigenvalues and Eigenvectors

Let $f:E\to E$ be an endomorphism where $(E,+,.)$ is a vectors space with dimension $K$. Every vector $x$ such that $f(x)=\lambda x$ with a $\lambda$ scalar and $x\in E\div \{o_E\}$ is said eigenvector of the endomorphism $f$ related to the eigenvalue $\lambda$ Eigenvalue and eigenvector are building blocks of reality

Dan terms: $\lambda$ = eigenvalue (num of x) $x$ = eigenvector (any number) homogeneous = (0,0)

Eigenspace

Let $f:E\to E$ be an endomorphism The set $V(\lambda)\subset E$ with $\lambda\in K$ defined as $V(\lambda)=e\{o_E\}\cup\{x\in E|f(x)=\lambda x\}$ This is said eigenspace of the endomorphism $f$ related to the eigenvalue $\lambda$. The dimension of the eigenspace is said geometric multiplicity of the eigne value $\lambda$ and is indicated with $\gamma_m$

Determining Eigenvalues and Eigenvectors

Let $f:E\to E$ be an endomorphism. Let $p(\lambda)$ be the order $n$ characteristic polynomial related to the endomorphism. The number of roots of $\rho(\lambda)$ is called algebraic multiplicity.

Introduction to Diagonalization

One variable for each line in a diagonal manner. Not all the mappings/matrices can be diagonalized, Need to have enough linearly independent columns of $P$.

Let $f:E\to E$ be an endomorphism. The matrix is diagonalizable if and only if it has n linearly independent eigenvectors:

• All the eigenvalues are distinct
• The algebraic multiplicity of each eigenvalue coincides with its geometric multiplicity

Symmetric Mappings

If the mapping is characterised by a symmetric matrix, then can prove that;

• The mapping is always diagonalisable
• The transformation matrix $P$ can be built to be orthogonal ($P^{-1}=P^{T})$. Also means the new reference system given by the eigenvectors is also a convenient orthogonal system