Skip to main content

2. Finite Automata

06/02/23

This content is basically state machines from Y1S1 (Bagley)

Deterministic Finite Automata (DFA)​

A deterministic finite automaton (DFA) A=(Q,Σ,δ,q0,F)A = (Q,\Sigma,δ,q_0,F)

  1. A finite set of states QQ
  2. A finite set of input symbols, the alphabet, Σ\Sigma
  3. A transition function δ∈Q×Σ→Qδ\in Q \times \Sigma \to Q
  4. An initial state q0∈Qq_0 \in Q
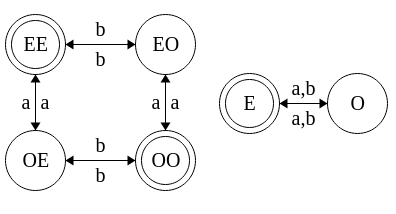
  5. A set of final states F⊆QF\subseteq Q An example is the following automaton D=({q0,q1,q2},{0,1},δD,q0,{q2})D=(\{q_0,q_1,q_2\},\{0,1\},δ_D,q_0,\{q_2\})

Initial state are sometimes called start states, and final states are sometimes called accepting states

Initial state is identified by putting an arrow →\to to the left of it and the final state are identified by a star ∗* . Initial states can also be final

Can also represent a DFA through a transition diagram

Language of a DFA​

  • The words accepted by a DFA is called the language L(A)L(A) of the DFA.
  • Once all symbols in the input word have been read, the word is accepted if the state is final, otherwise the word is rejected