3. Big-O (2)

10/02/23

Classification of Functions

Often need a way to group together functions by their scaling behaviour, and the classification should

• Remove unnecessary details
• Be (relatively) quick and easy
• Be able to deal with weird functions that can happen to runtime
• Still be mathematically well-defined

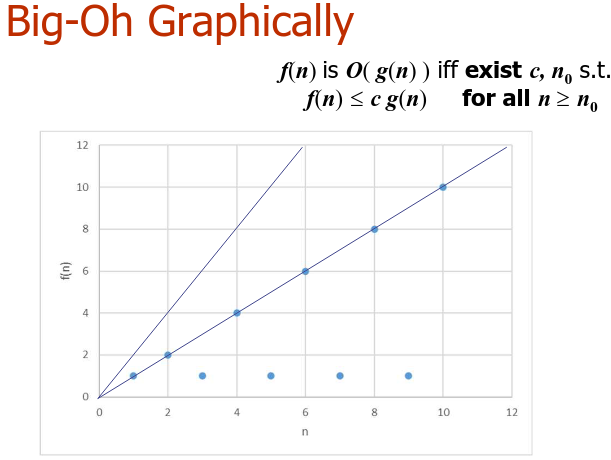
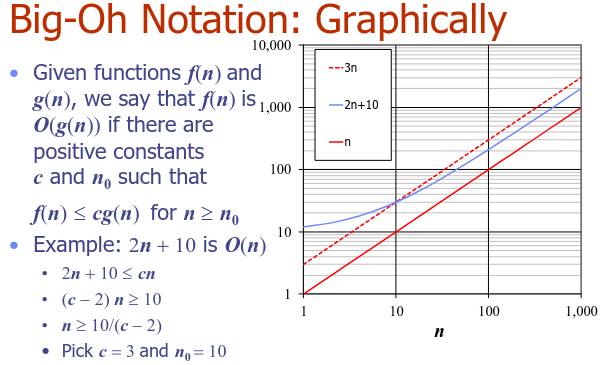
Ratios vs. big-Oh

• $f(n)$ can be $O(g(n))$ even if the ratio $f(n)/g(n)$ does not exist
• Therefore, big-Oh can be used in situations that ratios cannot
• The possibility of 'weird functions' means that big-Oh is more suitable than ratios for doing analysis of efficiency of programs

Binary relations, R, are characterised by potential properties:

• Reflexive - $xRx$
• Symmetric - $xRy$ iff $Rx$
• Transitive - $xRy$ & $yRz \to xRz$

Reflexive

• Trivial for any function
• $f(n)$ is $O(f(n))$
• as just take $c=1$, and use $\forall n.f(n)\le f(n)$

Symmetric

• Big-Oh is NOT symmetric
• $1$ is $O(n)$ but $n$ is not $O(1)$
• Only takes one counterexample to show that we cannot say it is symmetric

Transitive

• Given $f$ is $O(g)$ and $g$ is $O(h)$ we can show $f$ is $O(h)$

Set

• Big Oh as a binary relation is reflexive and transitive but not symmetric
• May help to thing of $O(n)$ as a set of functions with each function f in the set, $f\in O(n)$ satisfying $f$ is $O(n)$
• Behaves like $\subseteq,\in,\le$ but not $=$

Rules for quick big-Oh proofs

• Reverting the definition each time is time-consuming and error prone
• Better to develop a set of rules that allow us to very quickly find big-Oh

Multiplication Rule