8. Mergesort & Quicksort

27/02/23

Divide-and-Conquer

• General algorithm design paradigm
  • Divide - Divide the input data $S$ in two disjoint subsets $S_1$ and $S_2$
  • Recur - Solve the subproblems associated with $S_1$ and $S_2$
  • Conquer - Combine the solutions for $S_1$ and $S_2$ into a solution for $S$
• Base case is either size 0 or 1

Merge Sort

• On an input sequence (array/list) $S$ with $n$ elements consists of three steps:
  • Divide - Partition $S$ into two sequences $S_1$ and $S_2$ of about $n/2$ elements each
  • Recur - Recursively sort $S_1$ and $S_2$
  • Conquer - Merge $S_1$ and $S_2$ into a unique sorted sequence

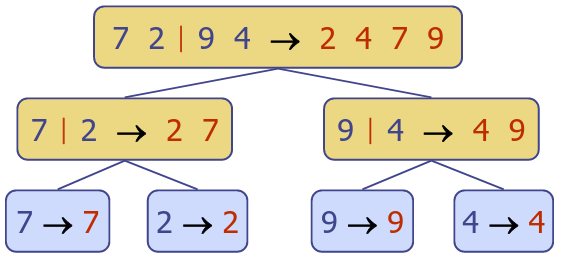
Merge-Sort Tree

• An execution of merge-sort is depicted by a binary tree
  • each node represents a recursive call of merge-sort and stores
    • unsorted sequences before the execution and its partition
    • sorted sequence at the end of the execution
  • the root is the initial call
  • the leaves are calls on sub sequences of size 0 or 1

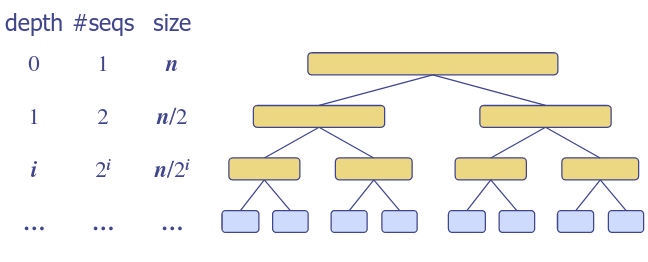
Analysis of Merge-Sort

• The height $h$ of the merge-sort tree is $O(\log n$)
• The overall amount of work done at all the nodes at depth $i$ is $O(n)$
  • partition and merge $2^i$ sequences of size $n/2^i$
  • make $2^{i+1}$ recursive calls
  • numbers all occur and are used at each depth
• Thus, the total running time of the merge sort is $O(n\log n)$

Quick-sort

• In mergesort the divide is simple but the merge is complicated. Quicksort replaces the merge part
• When the lists A and B are sorted and known to be in disjoin ordered ranges
• If A and B are stored as consecutive sub-arrays, then merge actually needs no work at all, just forget the boundary

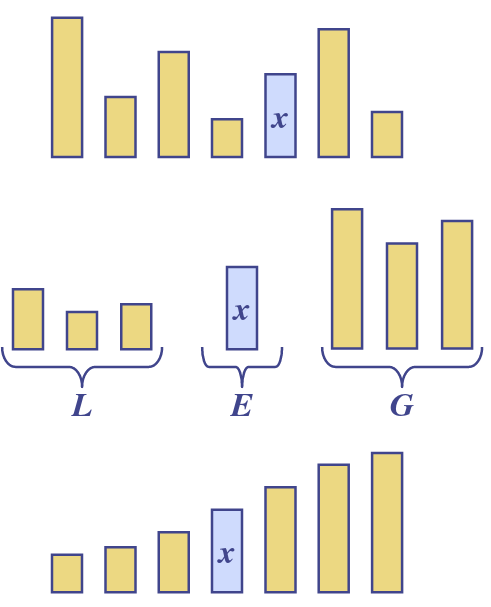
3-way split

• Quick-sort is a randomised sorting algorithm based on the divide-and-conquer paradigm
  • Divide - pick a random element $x$ (pivot) and partition $S$ into
    • $L$ elements less than $x$
    • $E$ elements equal to $x$
    • $G$ elements greater than $x$
  • Recur - sort $L$ and $G$
  • Conquer - join $L,E,G$

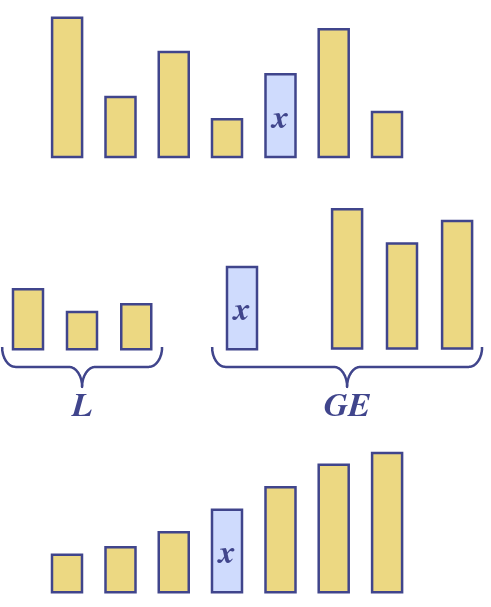
2-way split

• Divide - pick a random element $x$ (pivot) and partition $S$ into

  - $L$ elements less than $x$
  - $GE$ elements greater than or equal to$x$
• Recur - sort $L$ and $GE$
• Conquer - join $L,GE$

Partitions of Lists

• If storing $L,E,G$ as separate structures, we partition an input sequence as follows:
  • Remove, in turn, each element $y$ from $S$ and
  • Insert $y$ into $L,E,G$ or depending on the result of the comparison with the pivot $x$
• Each insertion and removal is at the beginning (or end) of the sequence, and hence takes $O(1)$ time
• Thus, the partition step of quick-sort takes $O(n)$ time

In-place - Means they only a little extra space is used to store data elements