15. Maps - Using binary search trees

24/03/23

Note intended to help with coding

• Global view of tree
  • Can look at entire tree in one go
  • Human seeing a picture of a (small) tree
• Local view of tree
  • What your code sees: "code perspective"
  • Code generally only sees a local portion of a tree and must work with that

Binary Search

• Search for an element within a sorted array is fast
  • Array to be searched is halved at each iteration, hence $O(\log n)$
• Only works because of the step of knowing whether to go left or right
• But arrays suffer from being slow, $O(n)$, to insert new elements. As needs to shift $O(n)$ elements to make room for them
• Search trees attempt to fix the inefficiency of insertion whilst keeping good $O(\log n)$ properties of binary search

Binary Search Trees

• Binary search tree is a binary tree storing key-value entries at its internal nodes and satisfying the following "search tree" property:
  • Let $u$, $v$, and $w$ be any three nodes such that $u$ is in the left subtree of $v$ and $w$ is in the right subtree of $v$;
  • $key(u)\le key(v) \le key(w)$
• External nodes do not store items, and likely are not actually implemented, but are just null links from the parent

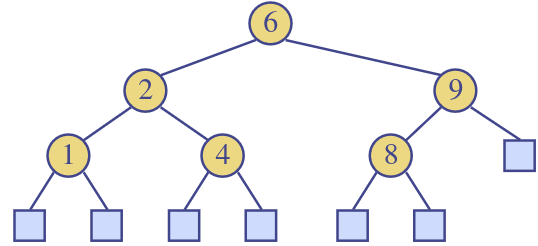
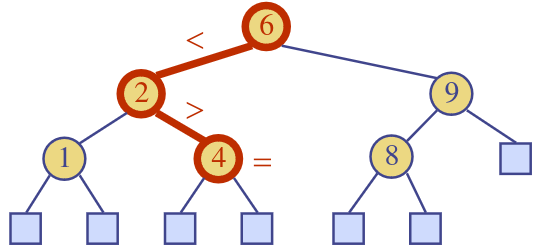
Search

• To search for the key $k$, trace a downward path starting at the root
• The next node visited depends on the outcome of the comparison of $k$ with the key of the current node
• If we reach a leaf, the key is not found and we return null

Recursive vs. Iterative

• Recursive programs are easier to implement, but less efficient because of the overhead of a function call
• For best efficiency, will need to convert to an iterative program
• while (test) {...}

Fundamental property of search tree - An inorder traversal of a (binary) search trees visits the keys in increase order. To access the minimum key, just need to 'always go left'

Insertion

• Insert $k$ where a get(k) would find it.
• If $k$ is already in tree then just replace the value, otherwise, $k$ is not already in the tree, and let $w$ be the leaf reached by the search

Deletion

• We remove $n$ from the tree and connect it to the parent. Still works if $n$ is a right child and has a left child
• For removing one with two children:
  1. Find the internal node $w$ that follows $n$ in an inorder traversal
  2. Copy $key(w)$ into node $n$
  3. Remove node $w$ and its left child $z$ (must be a leaf) by means of same procedure as before for one child

Balanced Trees

• Binary search trees: if all levels filled, then search, insertion and deletion are $O(\log N)$
• However performance may deteriorate to linear if nodes are inserted in order

Performance

• Binary search tree of height $h$ with $n$ items. The space used is $O(n)$. Methods take $O(h)$
• The height $h$ is $O(n)$ in the worst case and $O(\log n)$ in the best case

Self-Balancing

• Constantly re-structure of trees:
• Keep the trees height balanced so that the height is logarithmic in the size
• Performance always logarithmic

Issues

.....