7. Trees: Terminology, Traversals, Representations, and Properties
24/02/23
(Rooted) Tree - Tree is an abstract model of a hierarchical structure. Consists of nodes with parent-child relation.
Terminology
- Root - Node without parent
- Internal node - node with at least one child
- External node (leaf) - node without children
- Ancestors of a node - parent, grandparent etc
- Depth of a node - Number of ancestors (not counting itself)
- Height of a tree - Maximum depth of any node = length of longest path from root to a leaf
- Descendant of a node - Child, grandchild etc
- Subtree - Tree consisting of a node and its descendants
Traversals
- Visit each element precisely once, visit in some systematic and meaningful order
- For an array the natural way is a forwards scan
Preorder Traversal
- A node is visited before its descendants
- Application - Print a structured document
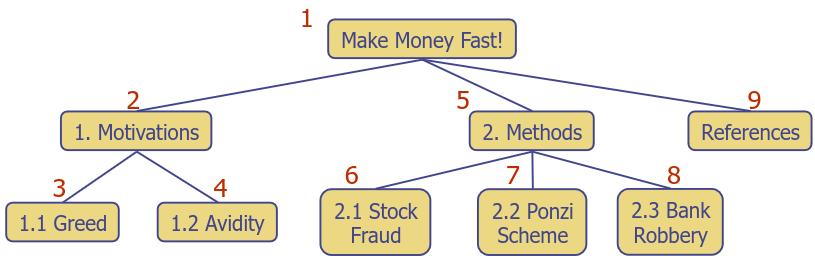
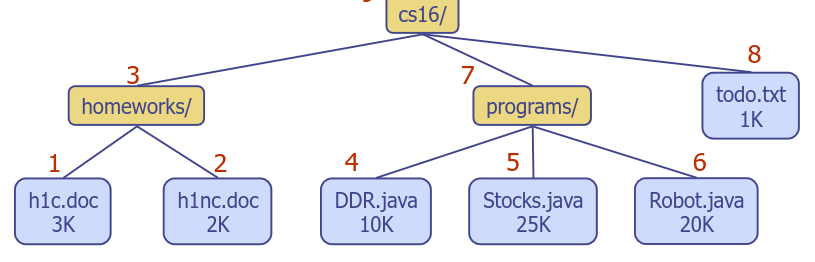
Postorder Traversal
- Visited after its descendants
- Application - Compute space used by files in a directory and its subdirectories
- (Used to evaluate arithmetic expressions)
Inorder Tranversal
- A node is visited after its left subtree and before its right subtree
- Application - Draw a binary tree by (x,y) coords
- (Used to print arithmetic expressions)
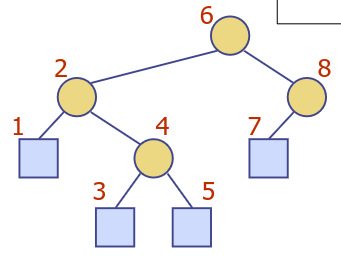
Tree types
Binary Trees
- Each internal node has at most two children
- The children of a done are an ordered pair - though one might be missing
- Call the children of an internal node left child and right child
- A proper binary tree has either two children or no children.
Arithmetic Expression Tree
- Binary tree associated with an arithmetic expression
- Internal nodes - (binary) operators
- external nodes - operands
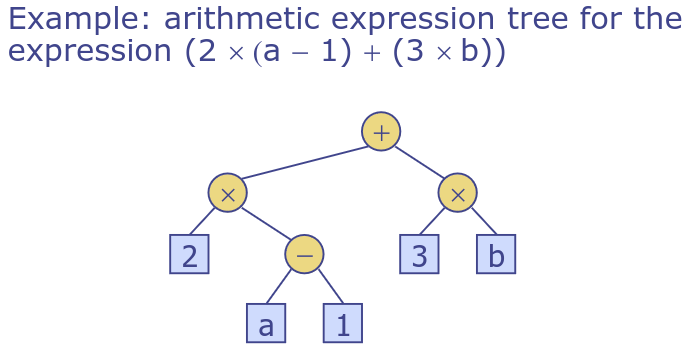
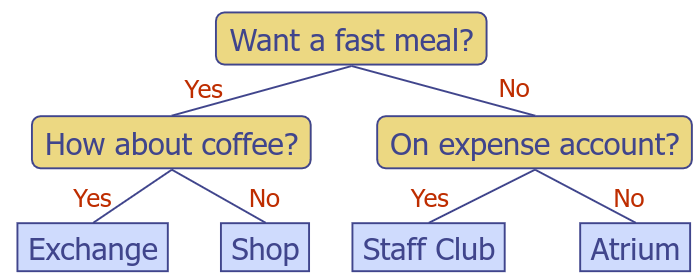
Decision Tree
- Binary tree associated with a decision process
- Internal nodes - questions with yes/no answers
- external nodes - decisions
Abstract Data Types (ADTs)
- Abstraction of a data structure
- Specifies - data stored, operations on the data, error conditions associated with operations
- An ADT does not specify the implementation itself
Concrete Data Types (CDTs)
- Actual data structure that we use
- ADT might be implemented using different choices for the CDT
- Choice of CDT will not be apparent from the interface (data hiding/ encapsulation)
- Choice of CDT will affect the runtime and space usage - and so is a major topic of this module
ADT & Efficiency
- Often the ADT comes with efficiency requirements expressed in big-Oh notation, yes some do not automatically force a particular CDT
- Typical of many library functions
- Such efficiency specifications rely on using the big-Oh family
Properties of perfect binary trees
- Said to be proper (full) if every internal node has exactly 2 children
- It is perfect if it is proper and all leaves are at the same depth; hence all levels are full
Height (h) is logarithmic in size (n)
- Very important property of a perfect binary tree