Skip to main content

12. Abstract Data Types - Stacks & Queues

13/02/23

ADT - Abstract Data Type

  • Only concerned with specifying the interface
  • Behaviour as seen from the outside
  • Specifies the methods provided - and possibly requirements on their complexity

CDT - Concrete Data Type (CDT)

  • Some structure and algorithm used for an actual implementation
  • Behaviour as seen form the inside

The Stack ADT​

  • The Stack ADT stores arbitrary (references to) objects
  • Insertions and deletions follow last-in first-out (LIFO)

Applications​

Direct applications

  • Page-visited history in a Web browser
  • Undo sequence in a text editor
  • Chain of method calls in the JVM

Indirect applications

  • Auxiliary data structure for algorithms
  • Components of other data structures

The Queue ADT​

  • Stores arbitrary objects
  • Insertions and deletions follow the first-in first-out FIFO scheme
  • Insertions are at the rear of the queue and removals are at the front of the queue

Applications of Queues​

Direct applications

  • Waiting lists
  • Access to shared resources
  • Event queues in GUIs and simulations Indirect applications
  • Auxiliary data structure for algorithms
  • Components of other data structures

Queue using Array as the CDT​

  • Use an array of size NN in a circular fashion
  • Two variables keep track of the front and rear
    • ff index of the front element
    • rr index immediately past the rear element
  • Array location rr is kept empty

Why not just use an Array instead of a Queue ADT?​

  • Conceptual Clarity
  • Self-Documentation
  • Safety of coding - prevents kludges
  • Potential Compiler Optimisations
  • Easier to change to a dynamically sizeable data structure

Narrow Vs. Wide ADT​

Narrow - small set of methods

  • Stack ADT
  • less flexible to use
  • more flexible to implement, hence maybe more efficient

Wide - Large set of methods

  • Java Stack
  • more flexible to use
  • Possibly more difficult to implement efficiently

Finding a good balance is a difficult design decision

Stacks and Queues by using linked lists​

Usage of Simplest linked list​

  • Could use them for any ADT
  • Observe that insertion and removal at head are very efficient, O(1)
  • If insert two elements then remove two elements, get LIFO .....

Priority Queues​

  • Stores a collection of entries
  • Each entry is a pair (key, value)

Total Order Relations​

  • Keys in a priority queue can be arbitrary objects on which an order is defined (between all different pairs)
  • Two distinct entries in a priority queue can have the same key

Comparator​

  • A comparator encapsulates the action of comparing two objects according to a given total order relation
  • A generic priority queue uses an auxiliary comparator
  • The comparator is external to the keys being compared
  • When the priority queue needs to compare two keys, it uses its comparator

Heaps​

  • A heap is a binary tree, storing key-value pairs at its nodes and satisfying the following properties:
    • Heap order - for every internal node v other than the root
    • Complete Binary Tree - Let hh be the height of the heap
  • The last node of a heap is the rightmost node of depth hh

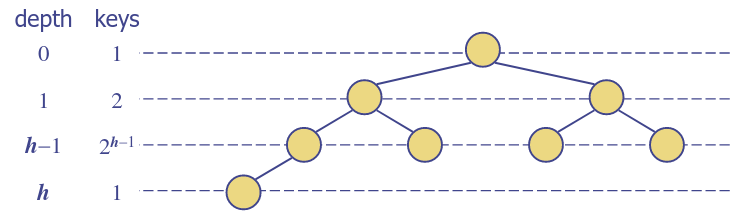
Height of a Heap​

Theorem: A heap storing nn keys has a height O(log⁡n)O(\log n) Proof: This uses just the complete binary tree property

  • Let hh be the height of a heap storing nn keys
  • The perfect binary tree of height h−1h-1 and 2h−12^h-1 nodes
  • Our trees has at least more

Heaps and Priority Queues​

  • Can use a heap to implement a priority queue
  • Store a (key, element) item at each node
  • Keep track of the position of the last node