13. Heaps & Maps

17/03/23

Heap

Insertion

• Method insertItem of the priority queue ADT corresponds to the insertion of a key $k$ to the heap
• The insertion algorithm consists of three steps
  • Find the insertion node $z$
  • Store $k$ at $z$
  • Restore the heap-order property

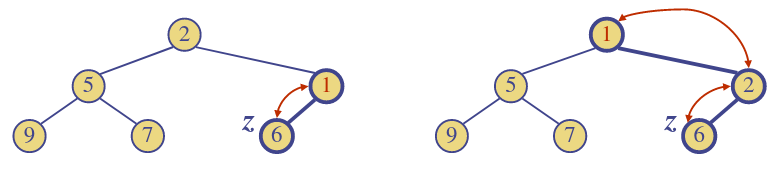
Upheap

• After the insertion of a new key $k$, the heap-order property may be violated
• Algorithm up heap restores the heap-order property by swapping $k$ along an upward path from the insertion node
• Upheap terminates when the key $k$ reaches the root or a node whose parent has a key smaller than or equal to $k$
• Since a heap has a height $O(\log n)$, upheap runs in $O(\log n)$ time.

Removal

• Method removeMin of the priority queue ADT corresponds to the removal of the root key from the heap
• The removal algorithm consists of three steps
  • Replace the root key with the key of the last node $w$
  • Remove $w$
  • Restore the heap-order property (discussed next)

Downheap

• After replacing the root key with the key $k$ of the last node, the heap-order property may be violated
• Algorithm downheap restores the heap-order property by swapping key $k$ along a particular downward path from the root
• Downheap terminates when key $k$ reaches a leaf or a node whose children have keys greater than or equal to $k$
• Since a heap has height $O(\log n)$ downheap runs in $O(\log n)$ time

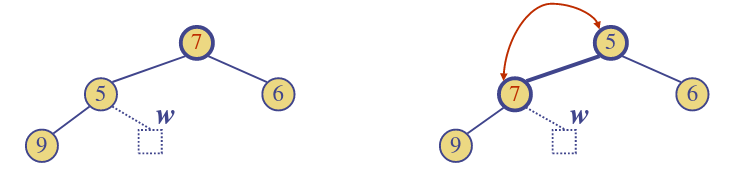
Array Heap Implementation

Similar to trees

• Can represent a heap with $n$ keys by means of an Array (or vector) of length $n+1$
• Links between nodes are not explicitly stored, instead for the node at index $i$:
  • the left child is at index $2i$
  • the right child is at index $2i+1$
  • the parent is at index $i/2$
• The cell at index 0 is not used
• No gaps when storing a heap
• Upheap and downheap just swap elements within the array

Heap sort

• Using a heap-based priority queue, can sort a sequence of n elements in $O(n\log n)$ time. Resulting algorithm is called heap-sort
• Heap-sort is much faster than quadratic sorting algorithms, such as insertion-sort and selection-sort

Has two stages:

1. Insert all elements into the heap one by one. Takes $n$ insertions with $O(\log n)$ each for a total of $O(n\log n)$
2. Remove all elements one by one, using removeMin(), hence obtaining them in sorted order. This takes $n$ removals with $O(\log n)$ each for a total of $O(n\log n)$

Do NOT confuse binary tree implementations of heaps with binary search trees!!

Maps ADT : Using lists

• A map models a collection of key-value entries that is searchable 'by the key'
• The main operations of a map are for searching, inserting, and deleting items
• Multiple entries with the same key are not allowed

MAP: Access any key PQ: Access only the minimum key

Can implement a map using unsorted list

• Store the items of the map in a list S (doubly-linked list) in arbitrary order
• and a size counter n, so getSize() is $O(1)$

Performance of a List-Based Map

• put would have taken $O(1)$ time if we could just insert the new item at the beginning (or end) of the sequence
• get and remove take $O(n)$ time since in the worse case (item not found) we traverse the entire sequence to look for an item with the given key
• The unsorted list implementation is suitable only for maps of small size, sorted list still $O(n)$